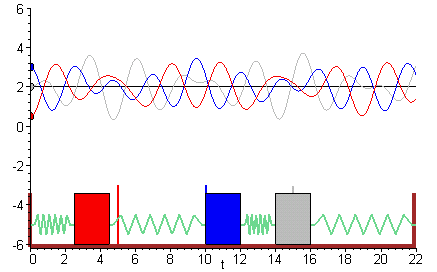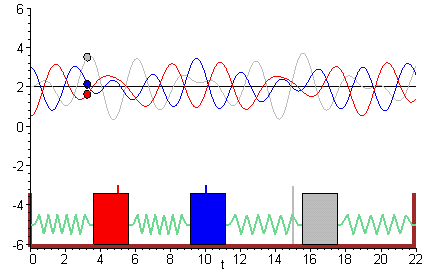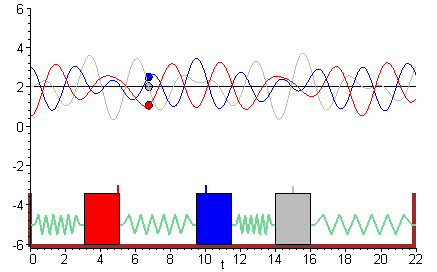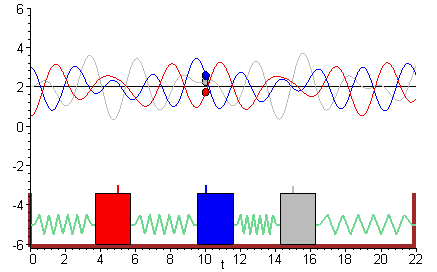
Coupled Spring-mass System

A Coupled Spring-Mass System. Three Masses coupled with Four spring without Damping. This figure shows the system to be modeled. Suppose that the masses are coupled to their immediate neighbors via identical light springs of unstreched length and force constant. We are going to teach you how coupled spring mass systems works vertically. A Coupled Spring-Mass System. Similarly if a second spring and mass are attached to the end of the first mass then the model becomes that of a system of second-order equations.

M1 d2x1 dt2 k1x1k2x1k2x2 m 1 d 2 x 1 d t 2 k 1 x 1 k 2 x 1 k 2 x 2 m2 d2x2 dt2.

For m_1 m_2 and x_1 ne x_2 If I write and solve that EoMs mddotx_1 k_0x_1kx_1 x_2 mddotx_2 -k_0x_2-kx_1x_2 I get omega sqrt4frac2k_0km. A Coupled Spring-Mass System. The scenario is the following we have. Two Coupled Harmonic Oscillators Consider a system of two objects of mass M. So springs with constant k_0 are compressedsprings push masses to their equilibrium then spring with k in mid is stretched pulls the masses to each other. This figure shows the system to be modeled.

Coupled Spring Mass System Scipy Cookbook Documentation

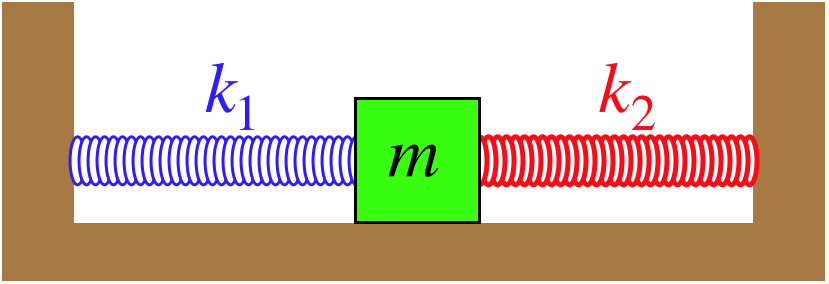
Coupled spring-mass system. 3 It is not hard to see that κx0 for any x 0. The spring has a spring constant of k and the length l of each string is the same as shown in Fig. This figure shows the system to be modeled.

Matlab Solution for Single Spring System. The energy is traded back and forth between the two oscillators. The springs coupling mass 1 and 3 and mass 1 and 2 have spring constant k and the spring coupling mass 2 and mass 3 has spring constant 2k.

The left end of the left spring is fixed. Figure 845 Coupled Oscillators With Three Springs. Spring-Coupled Masses Consider a mechanical system consisting of a linear array of identical masses that are free to slide in one dimension over a frictionless horizontal surface.

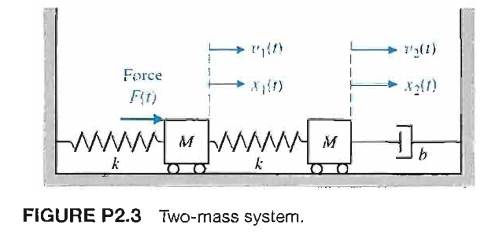
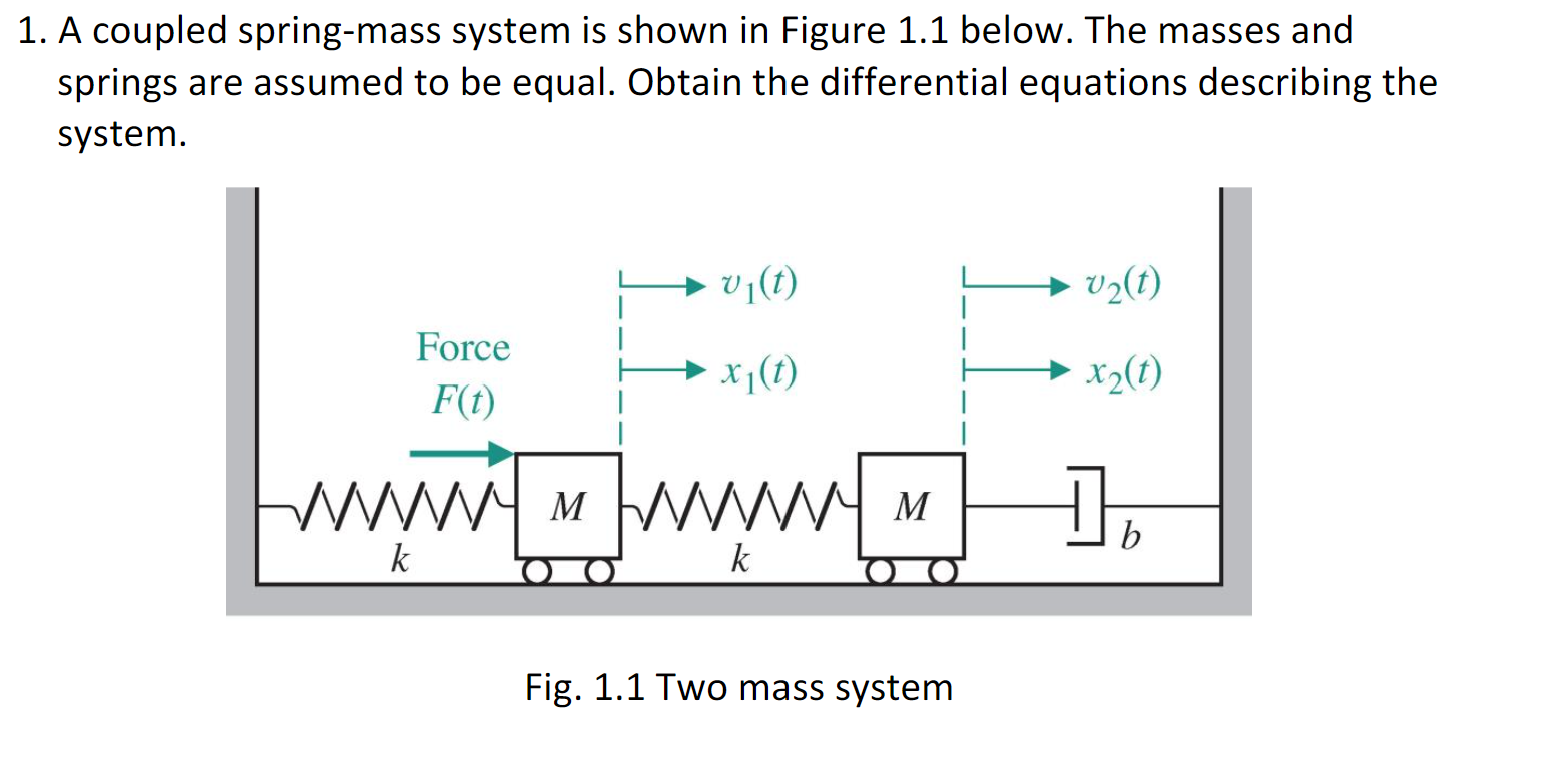
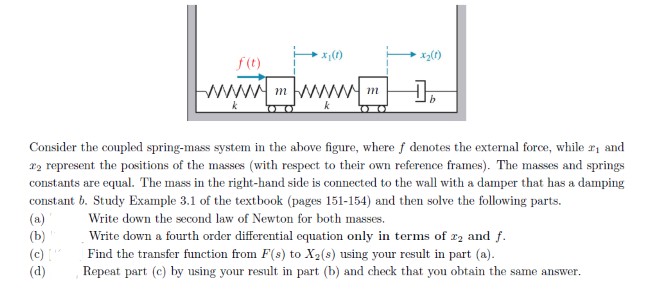
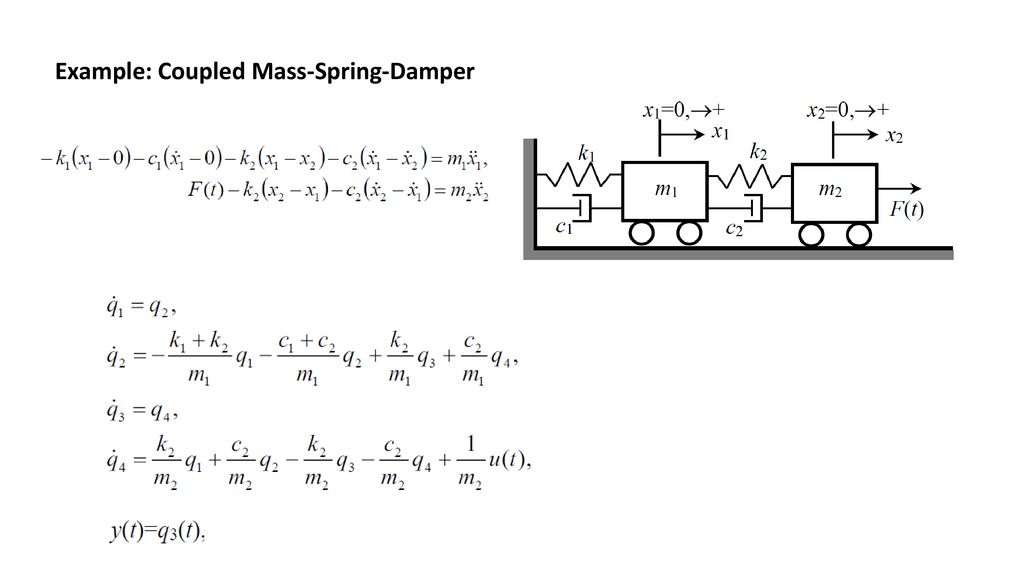
EXAMPLE 1 The First-Order System that Models Coupled SpringsBlocks. Rather than a single pendulum now let us consider two pendula which are coupled together by a spring which is connected to the masses at the end of two thin strings. As before we can write down the normal coordinates call them q 1 and q 2 which means Substituting gives.

Clearly the equation for the force on the left mass is identical to the example above Equation 846. We assume that the lengths of the springs when subjected to no external forces are L_1 and L_2. Similarly if a second spring and mass are attached to the end of the first mass then the model becomes that of a system of second-order equations.

The center of the coupling spring does not move. Consider the following figure. Three Masses coupled with Four spring without Damping.

At a given point the force that the right portion of the spring exerts on the left portion will be Txtand conversely the force that. Can be coupled by either the stiffness linear spring-mass system or inertia double pendulum matrices.

Coupled Spring Mass System Download Scientific Diagram

Coupled Mass Spring System How To Make It First Order Linear System Mathematics Stack Exchange

Two Spring Coupled Masses

Mass Spring Model Of A 2 Dof System Consisting Of Two Coupled Resonators Download Scientific Diagram

Solved 1 A Coupled Spring Mass System Is Shown In Figure P2 3 The 1 Answer Transtutors

Solved 1 A Coupled Spring Mass System Is Shown In Figure Chegg Com

Differential Equation Modeling Spring And Mass Sharetechnote

Spring Coupled Masses

Solved Consider The Coupled Spring Mass System In The Chegg Com

Scielo Brasil Analytic Solution To The Motion Of Mass Spring Oscillator Subjected To External Force Analytic Solution To The Motion Of Mass Spring Oscillator Subjected To External Force

Matthew T Clay Coupled Mass Spring System

Solving A Physically Double Spring Mass Energy System In Pthon

Two Coupled Oscillators

Mass Spring Model Of A 2 Dof System Consisting Of Two Coupled Resonators Download Scientific Diagram

State Space Representation Ppt Download

Analysis Of Coupled Mass Spring Damper System By Changing Spring Constant Mass And Force Semantic Scholar

Behavior Of A Coupled Mass System As Spring Stiffens

Coupled Oscillators Physicsthisweek Com

Coupled

Get Answer Suppose The Coupled Mass Spring System Of Problem 1 Figure 5 31 Transtutors

Coupled Oscillators Coordinates Ptw Youtube

Www2 Physics Ox Ac Uk

Differential Equation Modeling Spring And Mass Sharetechnote

1

8 4 Coupled Oscillators And Normal Modes Physics Libretexts

Two Spring Coupled Mass System Physics Stack Exchange

Paper Html

Lecture D34 Coupled Oscillators Spring

Coupled Spring Mass System Modeling And Simulation Lecture Handouts Docsity

Double Spring Mass Systems Matlab S Ode 45

2 Dof Oscillators

Solved P2 3 A Coupled Spring Mass System Is Shown In Figure Chegg Com

2 Pointsmy Notesask Your Teacherconsider The Coupled Itprospt

Mass Spring Html

Spring Mass System Proof Youtube

Coupledho Html

Www2 Physics Ox Ac Uk

Pdf Dynamics Of A Mass Spring Pendulum System With Vastly Different Frequencies Semantic Scholar

Teacher Pas Rochester Edu

Solved Consider The Coupled Spring Mass System On A Frictionless Table Shown Below The Two Masses M1 And 12 Each Have A Mass Of 1 Kg And The Springs Have Spring Constants Of K1

Mat 1235 Calculus Ii Section 9 1 Modeling With Differential Equations Ppt Download

A Handful Of Numerical Integration Techniques June 2014

Maintaining Specific Natural Frequency Of Damped System Despite Mass Modification

Fundamentals Of Vibration

Coupled

Vista Do Dynamic Analysis Of Wind Tower And Dimensioning Of Tuned Mass Damper Revista De Engenharia E Pesquisa Aplicada

Answered A Coupled Spring Mass System In The Bartleby

Analyze On A Coupled Beam Vibration System By Fem I Theory Scientific Net

1

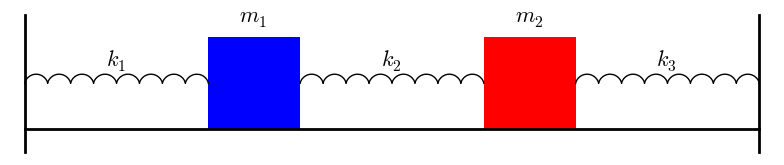
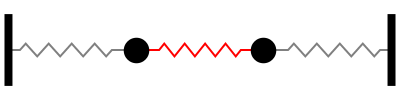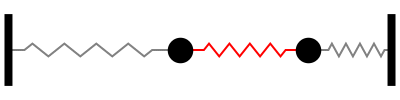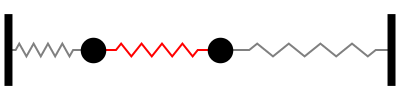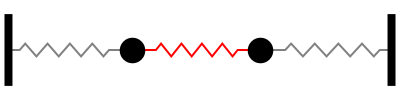
Suppose that the masses are attached to one another and to two immovable walls by means of three identical light horizontal springs of spring constant as shown in Figure 15.

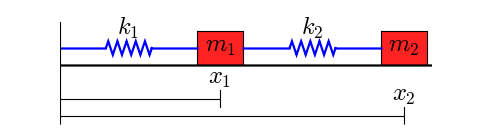
The solution to the eigenvalue. This figure shows the system to be modeled. The scenario is the following we have. Free vibrations of a MDOF vibration problem leads to an eigenvalue problem. We assume that the lengths of the springs when subjected to no external forces are L_1 and L_2. System 1 models the vibration dynamics of the coupled spring-block conguration. Coupled Spring Mass system. Using Newtons Second Law we can find equation of motion for each mass ie. At a given point the force that the right portion of the spring exerts on the left portion will be Txtand conversely the force that.

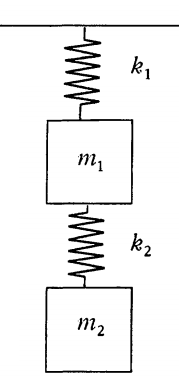
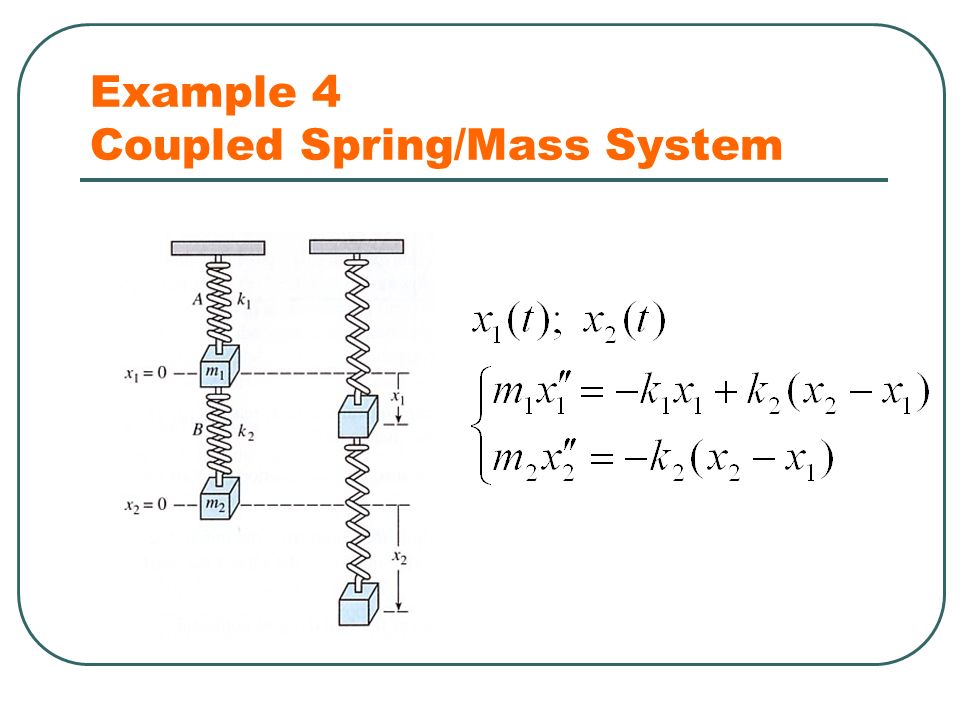
Hello I am having trouble trying to find the correct model for this coupled spring system. 3 It is not hard to see that κx0 for any x 0. A Coupled Spring-Mass System. Spring-Coupled Masses Consider a mechanical system consisting of a linear array of identical masses that are free to slide in one dimension over a frictionless horizontal surface. Can be coupled by either the stiffness linear spring-mass system or inertia double pendulum matrices. The spring has a spring constant of k and the length l of each string is the same as shown in Fig. Since the upper mass is attached to both springs there are tworestoringforcesactinguponitanupwardrestoringforce k 1x 1 exertedby theelongationorcompressionx 1ofthefirstspringanupwardforce k 2ðx 2 x 1Þ from the second springs resistance to being elongated or compressed by the amount x 2 x 1.